MODEL OF PROGRESSIVE VENTILATION
OF THE LATE PRECAMBRIAN-EARLY PALEOZOIC OCEAN
Marine Sciences Group
Department of Paleontology
University of California, Berkeley, California 94720
ABSTRACT
The development and evolution of redox conditions with depth in the open ocean is traced for the Late Precambrian-Early Paleozoic, using an oceanographic advection.diffusion model Wyrtki, 1961, 1962) and Henry's Law to predict redox conditions in the upper mixed layer and the main pycnocline for atmospheric oxygen contents from 1 to 100 percent PAL (Present Atmospheric Level of oxygen). Three climatic conditions: glacial, pre- to postglacial, and non-glacial (Wilde and Berry, 1982) define different pycnocline thicknesses at any given atmospheric oxygen content. The results indicate that the oceans and particularly the bottom waters of the continental shelves in equatorial regions remained anoxic and sulfidic, until the content of oxygen in the atmosphere reached about 3 to 5 percent PAL. With various ventilation strategies related to climate and water mass formation, anoxic waters without toxic dissolved sulfides could have been a significant intermediate water between oxic and sulfidic waters. At about 25 percent PAL, aquatic aerobic respiration could occur in the surface waters at high latitudes permitting the development of active predation. At this time, the anoxic but non sulfidic water could provide 8 haven for non-motile primitive animal life on the shelf and in the water column in advance of developing oxic conditions in the overlying water. Only at 45 percent PAL would the tropical surface waters be ventilated sufficiently to permit aerobic respiration. Even at 100 percent PAL, suggested for the Lower Paleozoic, global anoxic conditions on the shelf are predicted during warm climates due to the lack of oxygen ventilation in deep water.
INTRODUCTION
Berry and Wilde (1978) proposed that the oceans became progressively ventilated with atmospheric oxygen as a function of the effects of photosynthetic activity on oceanic composition and of changing climates on oceanic circulation. Their model was qualitative only using the evidence of time synchronous black shales to determine periods of global anoxicity. The following discussion presents an initial quantitative model of the ventilation. With appropriate geologic evidence, such a model may be used to define redox conditions in the global ocean for a given atmospheric oxygen composition and global climates as a function of time.
ATMOSPHERIC-OCEANIC EXCHANGE
Henry s Law states that the amount of gas dissolved in seawater is directly proportional to the partial pressure of that gas in the atmosphere (Kester 1975, p. 498-507; Broecker and Peng 1982, p. 110-116). Thus, the oxygen content of the oceans is limited to the oxygen concentration at oxygen and that in the ocean with depth, Wyrtki's (1961, 1962) techniques for generation of the oxygen minimum zone are used.
GENERATION OF REDOX PROFILES FOR THE OCEAN
The model assumes that the oxidative decay proceeds (Riley, 1951; Wyrtki, 1962, p. 13) as:
R = rate of decay at depth Z
Ro = rate at the surface
a = function of oxidized substance
Z = depth
and the steady state concentration of oxygen (Ox) can be found by the solution of:
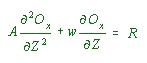 ......................................(2)
......................................(2)A = vertical exchange coefficient
w = vertical advection
Wyrtki (1961, p. 44) has shown how the temperature profile can be used to calculate w/A from the expression:
wT - A T/z = wTD................... (3)
T = potential temperature at given depth
TD= temperature at the depth of ascending water (base of the thermocline)
assuming, within the main thermocline, that (1) w is constant and (2) A is at a minimum. For the central part of the modern ocean he estimated that w = 2 x10-5 cm/sec and A = 0.5 cm2/sec were reasonable. These values are used in this paper for typical glacial climatic conditions: a main thermocline with a typical tropical temperature gradient of 20°C representing the difference between 25°C at the top of the thermocline at 100 m and 5°C at the base of the thermocline at 1000 m.
Reconstructions of temperature profiles during past non-glacial climatic conditions are highly conjectural. The Wilde and Berry (1982) nonglacial model based on mixing on temperature-salinity-density diagram develops two non-glacial situations based on the sources of deep water. Case A for the warmest climate has a main pycnocline from 100 to 3000 m. Whereas their Case B. pre- or post-glacial climate, has the main pycnocline from 100 to 1500 m. Table 1 shows the calculations for w/A (eq 3) for three climatic situations (A) non-glacial, (B) pre- or post-glacial, and (C) glacial.
An Interactive Redox Calculator to determine D.O. at depth for the various climates is available
Eq 2 is solved for the three climates. The upper boundary condition for depth (Z) is set at 50 m as an approximation of the depth of the photic zone. The upper boundary condition for oxygen (Ox) is set at the Henry's law oxygen saturation in the ocean for the particular atmospheric oxygen concentration or PAL. The upper boundaries are fixed for all three climates. The depth of the lower boundary of the pycnocline varies with climate from a maximum depth of 3000 m (non-glacial) to a minimum depth of 1000 m (glacial). The concentration of oxygen at the lower boundary never exceeds the absolute value at the surface. An equivalence of upper and lower boundary concentrations for oxygen would simulate the modern situation in the tropics and would yield the most ventilated conditions. This is.accomplished, today, by lateral advection of oxygen from higher latitudes for the deep water below the pycnocline. The deep water forms at the surface in the colder higher latitudes so has a higher initial concentration. In the modern ocean, the consumption of oxygen in the deep water in transit to the tropics reduces the concentration to that approximating the absolute value at saturation in the warmer tropical surface waters (Arons and Stommel, 1967; Kuo and Veronis, 1973). A Similar oceanographic origin for deep water is assumed for the model. App. A gives the solution of eq (2) and a sample calculation.
From these boundary conditions, an oxygen equivalent profile for the pycnocline is generated with the possibility for both positive and negative oxygen equivalents. Positive equivalents resect model oxygen concentrations, whereas the negative values reflect the equivalent oxygen demand or anoxicity. Negative oxygen equivalents are used rather than converting to some redox scale, such as Eh or pE, to preserve the familiar shape of the oxygen profile used in the oceanographic literature.
Negative equivalent oxygen concentrations.--Redfield, Ketchum, and Richards (1963, p. 42-43) showed thermodynamically that with the depletion of oxygen due to consumption by organic matter, other constituents in seawater replace oxygen as the principal oxidant. This would be the chemical situation for the generation of model negative oxygen equivalents. The sequence of major oxidants in seawater, in order of increasing anoxicity (Stumm and Morgan, 1970, p. 318), are--oxic conditions: (1) oxygen; anoxic conditions: (2) nitrogen compounds, (3) sulfate, and (4) carbon dioxide. Thus for increasingly negative oxygen equivalents, a generalized zonation may be established in the model redox profiles based on the sequence of available oxidants. To quantify oxygen equivalents, Redfield, Ketchum, and Richards (1963, p. 46) used the stoichiometric ratio of the particular oxidant to that of phosphate-phosphorous in the standard plankton photosynthetic reactions in seawater to show the changes in composition of the products of decay under both oxic and anoxic conditions. Thus the amount of phosphate generated is used to predict the quantity of oxygen that would have been consumed, if oxygen had been present. The basic equations (Richards, 1957, 1965) are:
[(CH2O106(NH3)l6(H3PO4)] + 138 O2 =
106 CO2 + 122 H2O + 16 HNO3 + H3PO4
02/P = - 138; NO3--N/P = 16; CO2--C/P = 106 (4)
ANOXIC CONDITIONS
Denitrification
[(CH2O106(NH3)l6(H3PO4)]+ 94.4 HNO3 =
106 CO2 + 177.2 H2O + 55.2 N2 + H3PO4
NO3--N/P = - 94.4 (5)
to
[(CH2O106(NH3)l6(H3PO4)]+ 84.8 HNO3 =
106 CO2 + 148.4 H2O + 42.4 N2 + 16 NH3 + H3PO4
NO3--N/P = - 84.8 (6)
Richards (1965, p. 625) found at Lake Nitinat that about half the ammonia (eq 5) is converted to N2, so that the actual coefficient for nitrate in denitrification is between 94.4 and 84.8.
[(CH2O106(NH3)l6(H3PO4)]+ 53 SO4 2-) =
106 CO2 + 106 H2O + 53 S2- + 16 NH3 + H3PO4
SO4 2-/P = - 53 (7)
The Redfield, Ketchum, and Richards (1963) method assumes that all nitrate comes from the oxidative decay of "ammonia" in the standard plankton. The amount of nitrate generated during oxic decay of plankton, depleting the oxygen (eq 4), would be
[HNO3] = 16 [02; surface]/138 (8)
With excess organic matter in the absence of oxygen, this nitrate would become the next available oxidant. The nitrate would generate additional phosphate stoichiometrically by oxidation of more plankton. The amount of phosphate generated during the depletion of the nitrate would depend on the nitrate reduction mechanism indicated in eq 5 or eq 6 or some combination of the two or
[HNO3]= [HNO3 eq. 8]/ 84.8 to 94.4 (9)
This phosphate concentration times 138 gives the amount of oxygen that would have yielded that amount of phosphate under oxic conditions (eq 4). That value in terms of oxygen would be the oxygen equivalent (oxidation equivalent of Richards, 1965) at that site or the negative oxygen value for the anoxic consumption of all of the nitrate.
[02, equivalent] = - 138 [H3PO4, eq 9] (10)
For this model, equatorial surface conditions of 25°C and 35 per mil will be assumed. This yields a Henry's Law saturation concentration of about 5 mL/L (230 µmoles/kg). So by the above argument, at 100 percent PAL in the tropics, the upper nitrate/sulfate boundary would be between --0.9 and--1.0 mL/L oxygen (28 µmoles nitrate reduced). A similar argument can be made for the generation of the lower nitrate/sulfate boundary using the polar surface concentration of oxygen. As polar water is colder and contains more oxygen, the nitrate content from eq (8) would be higher, and the boundary would be more negative.
With the continued introduction of organic matter after the depletion of oxidized nitrogen compounds, the next oxidative process, sulfate reduction, would begin. Sulfate is conservative in the present ocean with a value at 35 per mil of 28,240 ''moles/kg (Quinby-Hunt and Turekian, 1982). Total sulfate reduction would produce 28,240/53 = 533 µmoles/kg P. the equivalent of 73,530 µmoles/kg O2. Thus the sulfate depletion boundary would be at--1600 mL/L, being the same at both the upper and lower boundaries because of the conservative nature of sulfate in seawater. Due to the low free energy of sulfate reduction (Stumm and Morgan, 1970, p. 318), oxidized sulfur as sulfate would have formed in the ancient ocean before free oxygen appeared in the atmosphere (Garrels and Perry, 1974).
Question of residual anoxicity and preformed nutrients.--As a first approximation, the Redfield,
Ketchum, and Richards (1963) assumption of nitrate of oxidative origin (eq 4) will be used to
establish the boundary of the first anoxic zone where oxidized nitrogen compounds are depleted.
If only the Henry's Law surface concentration of oxygen is used to generate the nitrate, then at
low percent PAL there would be little nitrate, and thus the oxygen equivalent of nitrate would
approach zero. However, nitrate and nitrite can be synthesized from ammonia and maintained
even at low atmospheric oxygen levels by nitrifying bacteria (Vaccaro, 1965, p. 377-383; Broda,
1975, p. 92; Blackburn, 1983, p. 75). In the present ocean, where nitrate is stable below the
photic zone, the Henry's Law saturation value in the ocean is approximately equal to an
atmospheric level of 5 percent PAL. This suggests that nitrifying bacteria could function at such
levels, producing nitrate.
Before the build-up of oxygen in the atmosphere, according to the Sillen-Garrels models (Sillen, 1961; Garrels and Perry, 1974), oxygen derived through photosynthesis would be used sequentially to oxidize more reduced species. Thus sulfate and carbonate in seawater would already be in their present state of maximum oxidation prior to the development of free oxygen in the atmosphere. Thermodynamically, oxidized nitrogen compounds would be the last to be formed just prior to free oxygen developing in the atmosphere. Ideally, all the combined nitrogen would be as nitrate in the sequence ammonia to nitrite to nitrate, as free oxygen developed in the atmosphere. But this is not true even at 100 percent PAL, where nitrate is about 65 percent of the combined oceanic nitrogen (Vaccaro, 1965, p. 366). A complicating factor is the existence of relatively inert dissolved nitrogen positioned so it forms a large sink between oxidized nitrogen as nitrate and nitrite and reduced nitrogen as ammonia. As noted above, during denitrification or nitrate reduction the end product is both nitrogen and ammonia (eqs 5 and 6) with the amount converted to dissolved nitrogen effectively taken out of the active pool. On the other hand, nitrogen fixing bacteria can form ammonia directly from dissolved nitrogen. This would add ammonia to the oceans at any stage of the sequential oxidation of nitrogen compounds (Saino and others, 1983). Conversely, nitrification of ammonia to nitrite and nitrate in the dark has been demonstrated experimentally (Harvey, 1960). Also, photosynthetic organisms prefer ammonia as a nutrient (Eppley, Rogers, and McCarthy, 1969), so that ammonia would be readily consumed in the photic zone. Thus the amount and the partition of species of reactive nitrogen (total combined nitrogen as ammonia, nitrite, and nitrate) residual from the ocean in contact with the preoxic atmosphere would be difficult to estimate. As nitrate is the terminal oxidation state for combined nitrogen, it would seem unlikely that the amount of nitrate in seawater would be greater in the ancient ocean than in the well-ventilated modern ocean. The question is whether the partition of nitrogen compounds in the early ocean equilibrated at low PAL was buffered by various nitrogen bacteria and photosynthetic organisms to near modern values. Such information would be useful in determining the rate of ventilation of the atmosphere. For example, at low PAL, biogenic oxygen that otherwise might be added to the atmosphere may have been used to maintain adequate nitrate levels in the ocean.
LIMITATIONS OF THE MODEL
Wyrtki's (1961, 1962) advection-diffusion model is modified here to generate oxygen (positive) and oxygen equivalent (negative) profiles with depth. Any interpretations based on this use should consider the following limitations and assumptions. In general, the major uncertainties pertain to the anoxicity of deep water. The model best reflects conditions in the surface mixed layer and the upper pycnocline. Thus the interpretations and implications of the model with respect to shelf conditions would have the most validity.
A. The model is strictly one-dimensional (depth dependence only). It assumes that initial conditions are governed by the Henry's Law saturation of the overlying ocean at given PAL with overlying surface organic production providing reduced matter for vertical settling and the development of anoxicity. Thus, this model yields the most oxygenated conditions as residual anoxicity and lateral advection are ignored. Actual conditions in the water column below the pycnocline may have been more anoxic, due to bacterial decay during lateral advection from high latitudes to the tropics. Arons and Stommel (1967) and Kuo and Veronis (1973) estimate a "best fit" oxygen consumption rate of 0.002 mL/L per year for the modern ocean. Thus for water with an initial oxygen content of 1 mL/L, a transit time of only 500 yrs would be sufficient to consume all the dissolved oxygen in the deep water.
B. The paleotemperature profiles and water mass volumes used here are simplistic considering only three generalized climatic conditions. Thus, the actual w/A values most likely would vary with latitude. An equatorial location was chosen to maximize the temperature contrast of the deep waters, while maintaining uniform surface temperatures.
C. The ventilation efficiency is not estimated during buildup of oxygen in the atmosphere (modern value about 45 percent). Interaction of any residual anoxicity with oxygenated water was not considered. Also, a lengthy Precambrian glaciation, even at low PAL, could ventilate the deep-waters sufficiently to destroy prior anoxicity.
D. The value (eq 1) is set constant at 2.5 X 10-5 (from Wyrtki, 1962, p. 16) and to give the best fit to modern data in the tropics. This value is a property of the substance oxidized and ideally should vary with depth as the more easily oxidized material is depleted at shallower depths.
Thus would decrease with depth. However, the shape of the redox curve is sensitive to changes both in and w/A (Wyrtki (1962, p. 15-16 and 20). As noted above, complications due to the geographical variation in w/A, for a given climate, can be avoided by using an equatorial location. Whether a varies with climate or time is beyond the scope of this paper. But the equatorial location of the calculations should minimize any temperature related change in the refractory nature of material oxidized, as the surface temperature for all three climates is the same.
E. Due to the paucity of samples and datable marine rocks before the Phanerozoic, isotopic values are not available for most of the time range covered by the model. However, marine isotopic data do show progressive enrichment in 13C and depletion in 34S from the Late Precambrian through the middle Paleozoic (Holler, 1984; Schidlowski and Junge, 1981; Veizer, Holser, and Wilgus, 1980; Schidlowski, Junge, and Pietrek, 1977). This could be interpreted, particularly for the sulfur system, as corroborating the progressive ventilation of the ocean as indicating the removal of significant anoxic waters by the end of the Devonian. Use of the model for global reservoir calculations for oceanic carbon or sulfur, by extrapolating the profiles at any given PAL to volumes, should be tempered by the uncertainties in the latitudinal distribution of oceanic depths with time and temperature with climate as well as fixing the depth of the deep oxic-anoxic boundary as noted above.
MODEL RESULTS
The Wyrtki model was solved (figs. 1, 2, 3, app. A, and table 2 give sample calculations) for various atmospheric oxygen concentrations from to 100 percent PAL for Equatorial surface conditions (25°C, 35 per mil). For each atmospheric condition, profiles were generated for three thermal and density profiles associated with non-glacial, pre- and post-glacial, and glacial climatic conditions (see table 2). The atmospheric conditions for each example produce the appropriate Henry's Law oxygen concentration in the water column from tile surface to 50 m (the model depth of the photic zone) and at the base of the pycnocline. Such assumptions of deep ventilation may be valid only for glacial conditions, particularly at low concentrations of oxygen in the atmosphere. In any case, assumption of Henry's Law saturation at depth yields the most positive (oxidative) redox conditions. The profiles are given over two ranges of depths: (1) 0 to 4000 m (fig. 1), indicating the extent of anoxicity in the vertical water column in the open ocean and (2) 0 to 300 m (fig. 2), simulating the possible conditions on the continental shelf.
As expected, the model generates the most ventilated conditions at any given atmospheric oxygen level for glacial climates due to their increased temperature gradient and compressed pycnocline (table 1). The ventilation calculated during glacial times probably is low, as the increased solubility of oxygen in seawater with decreasing temperature was not considered for deep water. The model indicates that waters above the shelf would be oxic to 100 m as early as about 30 percent PAL during glacial times, but as late as about 50 percent PAL during a non-glacial climate. The occurrence of any given ventilation situation depends on the timing and sequence of climatic variation. Also, the model predicts the maximum extent of anoxicbut nonsulfidic waters over the shelf would occur during glacial climates, as shown in figure 2, A and B. During glacial times, the combination of lower sealevels and ventilation at relatively shallow depths move tile sulfidic zone to the shelf edge or deeper. This would expand habitability of the shelf by moving the potential of the upwelling of toxic sulfidic waters farther off-shore. Such a situation would have significant evolutionary consequences. This implies that the maximum stress to oceanic aerobic biota would be during non-glacial times with sulfidic waters on the shelf. Thus maximum expansion of aerobes might occur during glacial climates. Figure 3 demonstrates how the zone boundaries on the shelf could fluctuate with variations in the depth of deep ventilation even at 100 percent PAL.
EVOLUTIONARY IMPLICATIONS
The modeling of the progressive ventilation of the ocean from 1 percent PAL to 100 percent PAL yields changing redox conditions which have geologic and oceanographic significance with respect to the initiation and sequence of evolutionary events in marine biota. The model best predicts conditions occurring in the mixed layer and the upper portion of the main pycnocline of the ocean. Thus, the consequences of these conditions would be reflected in the organisms living in the upper water column and in the intersecting benthic boundary layer.
Of particular ecologic interest is the possibility of anoxic waters in the water column, where nitrogen compounds act as available oxidants intermediate between oxygen and sulfate reduction. In general, chiefly by analogy with the modern Black Sea or the Cariaco Trench, anoxic waters are considered to be synonymous with sulfidic or reduced sulfur waters (Ryan and Cita, l977; Hashimoto and others, 1983). Accordingly, usually only two types of water masses: oxic and anoxic; and three types of biofacies: (1) aerobic [>1 mL/L], (2) dysaerobic [0.1 to 1 mL/L]; and (3) anaerobic [< 0.1 mL/L] (Rhodes and Morse, 1971, Byers, 1977) based on redox potential are considered. However, evidence from the modern well-ventilated ocean suggests that a two-fold classification is too simple. In particular, anoxic parts of the modern ocean have redox zones not governed by reduced sulfur species. For example, in the 100 m thick "oxygen minimum zones" in the Eastern Tropical Pacific (Goering, 1968; Cline and Richards, 1977; Anderson and others, 1982); and in the Arabian Sea in the Indian Ocean (Warren, 1981; Qasim, 1982); nitrogen reduction not oxygen reduction is the major process consuming organic matter (Broecker and Peng, 1982, p. 141). In the modern ocean, due to ventilation of deep water as a result of the present cold climate, the denitrification zone is underlain by a nitrification zone produced by oxygen adverting from below (Thomas, 1966, Wooster, 1967). However, during warm climates and prior to the complete ventilation of the ocean, deep waters probably were not reoxygenated to the extent they are during glacial climates. Such conditions are postulated for the Lower Paleozoic (Berry and Wilde, 1978).
Thus, mildly anoxic waters, that is without reduced sulfur compounds, seem feasible in seawater during ventilation. Such anoxic-non sulfidic waters would be favorable to nitrogen requiring organisms due to presence of preferred nitrogen compounds (Eppley, Rogers, and McCarthy, 1969) in the absence of the often toxic sulfides and other reduced sulfur species.
Significant oxidation steps in progressive ventilation.--The level of oxygen in the atmosphere would have to be above 5.5 mL/L or 2.8 percent PAL {Polar} to 10 mL/L or 5 percent PAL {Tropical} to have sufficient oxygen dissolved in seawater (0.22 mL/L or 10 µmoles/kg) for oxygen to act as an oxidant (Devol, 1978). To be above the Pasteur Point of 2 mL/L (Fenchal and Blackburn, 1979, p. 48) to permit aerobic respiration in seawater, the atmosphere must be at 50 mL/L or 25 percent PAL {Polar} to 90 mL/L or 45 percent PAL {Tropical}. Due to the oxygen demand of organic matter derived from photosynthetic organisms, which add oxygen to the atmosphere, any oxygen concentration in the atmosphere below about 5 percent PAL would be insufficient to maintain oxic conditions in the water column except in the uppermost few meters. For an atmosphere 5 to 25 percent PAL probably only the wind-mixed upper ocean of the photic zone (about 50 m) could support oxygen oxidation but not aerobic respiration.
Proposed evolutionary scenario with progressive ventilation.--Until about 5 percent PAL the ocean did not support oxic reactions, and reduced-sulfur compounds probably dominated in the ocean. Once non-oxic but non-sulfidic oxidation was supported, shallow water sessile organisms requiring low oxygen could develop, feeding on algae or bacteria such as sulfur-based chemoautotrophes (Berry and Wilde, 1982) unaffected by anoxicity. New aerobic sessile animals may have evolved from shallow water dwelling precursors which would be driven to deeper water as the denitrification zone expanded over the shelf. The presence, on the shelf, of the toxic sulfidic waters would limit sessile aerobes to intertidal and shallow waters.
Above 5 percent PAL, oxidation could persist in the upper 50 m. The oxic zone would be entirely within the photic zone until 10 percent PAL. With ammonia available in underlying anoxic non-sulfidic waters within the photic zone (having been derived from the decomposition of both settling aerobic organisms and local anaerobic organisms), the growth of photosynthetic organisms would not be limited by nitrogen to the degree they are today, with a dependence on upwelling for resupply. Such groups may have been limited chiefly by phosphorus. When photosynthesis occurred within the denitrification zone, the limitation on growth may have been the seasonal variation in the duration of daylight with latitude. In any case, conditions of high and geographically uniform nutrient supply could indicate much higher photosynthetic activity than at present. This high level of productivity would accelerate the oxygenation of the atmosphere. On the other hand, high productivity would cause anoxicity to persist longer in the near surface ocean below the wind-mixed layer due to the large volume of organic matter. Once the atmosphere was oxygenated sufficiently to ventilate the surface layer below the photic zone, modern nutrient limitations with respect to the primary food webs must have obtained. Accordingly, ventilation of the atmosphere by oxygen derived from marine sources probably slowed.
From about 25 to 45 percent PAL active motion by animals could develop as respiration would be permitted in the surface layer. The early respirors probably were grazers living in the photic zone. Because of the negative correlation between temperature and saturation (Weiss, 1970), it is likely that oxygen respiration developed initially in high latitudes in colder more oxygenated surface waters. Favorable conditions for respiration would move equatorward with increasing oxygen in the atmosphere. As continued ventilation drove the nutrient supply well below the photic zone, predation may have developed as a response to the reduction in the quantity and the more localized distribution of the algal food supply. Initially, predation may have developed innocently, as it would be difficult to distinguish simple sessile animals living symbiotically with algae from the algae proper. The upper denitrification zone would be a haven for sessile animals which evolved during more anoxic condition near the surface. Those animals living in ~he more oxic surface layers may have developed some armor or housing to protect or minimize the effect of predation. At this time planktonic growth would develop the patchiness seen in the modern oceans. The development of the zooplankton niche into the food web, with the increasing ventilation of the surface layers, may have triggered more active predation. The rapid evolution of shell, carapaces, et cetera as a protective strategy would greatly increase the chance of fossilization. The availability of nitrogen compounds in shallow anoxic zones suggests that nitrogenous material such as chitin could be the most readily available protective substance.
Even at 100 percent PAL, the potential for anoxicity still exists as a function of climate and previous redox status of the ocean (fig. 3). This can be generated as a residual anoxic layer from previous low oxygen conditions (Berry and Wilde, 1978) prior to ventilation by glaciations or as a return to anoxic conditions caused by reduction due to unoxidized organic matter raining down in a poorly ventilated ocean (Wilde and Berry, 1982).
For the post mid-Paleozoic world, fluctuations in atmospheric oxygen from present levels, predicted by the global models such as those proposed by Kump and Garrels (1986), would also be translated into variations in the chemistry of the oceans. These fluctuations may account for some of the changes in oceanic chemistry noted by Holser (1984). Such changes also may have evolutionary implications for marine organisms as seen in various extinction events after the initial ventilation (Wilde and Berry, 1984; Wilde and Berry, 1986).
ACKNOWLEDGMENTS
I wish to thank Dr. M. S. Quinby-Hunt for her tireless efforts in making the chemical part of this paper intelligible. Dr. A. T. Dengler checked the mathematics of the model and made many useful simplifying suggestions. Prof. W. B. N. Berry offered continuing support. M. A. Krup did her usual outstanding job in illustrating and managing the manuscript. This is contribution MSG-85-021 of the Marine Sciences Group and is part of the Black Shale Project, a cooperative effort of the Department of Paleontology and the Chemical Analytical Group of the Los Alamos National Laboratory.
REFERENCES
Anderson, J. J., Okubo, A., Robbins, A. S., and Richards, F. A., 1982, A model for nitrite and nitrate distributions in oceanic oxygen minimum zones: Deep-Sea Research, v. 29, p. 1113-1140.
Arons, A. B., and Stommel, H., 1967, On the abyssal circulation of the world ocean-III. An advection-lateral mixing model of the distribution of a tracer property in an ocean basin: Deep-Sea Research, v. 14, p. 441-457.
Berkner, L. V., and Marshall, L. C., 1967, The rise of oxygen in the earth's atmosphere with notes on the Martian atmosphere: Adv. Geophysics, v. 12, p. 309-331.
Berry, W. B. N., and Wilde, P., 1978, Progressive ventilation of the Oceans--An explanation for the distribution of the Lower Paleozoic Black Shales: Am. Jour. Sci., v. 278. p. 257-275.
1983, Evolutionary and Geologic Consequences of Organic Carbon Fixing in the Primitive Anoxic Ocean: Geology, v. 11, p. 141-145.
Blackburn, T. H., 1983, The microbial nitrogen cycle, in Krumbein, W. E., ea.: Microbial Geochemistry, Oxford, England, Blackwell, p. 63-89.
Brandhorst, W., 1959, Vitrification and dentrification in the eastern tropical North Pacific: Jour. du Counseil Permanent Internat. Exploration du Mer, v. 25, p. 3-20.
Broda, E., 1975, The History of Inorganic Nitrogen in the Biosphere: Jour. Molecular Evolution, v. 7, p. 87-100.
Broecker, W. S., and Peng, T.-H., 1982, Tracers in the Sea: Palisades, N.Y., Eldigio Press, 690 p.
Byers, C. W., 1977, Biofacies patterns in euxinic basins: a general model, in Cook, H. E. and Enos, P., eds., Deep-water carbonate environments: Soc. Econ. Paleontologists and Mineralogists Spec. Pub. 25, p. 5-17.
Cline, J. D., and Richards, F. A., 1972, Low oxygen concentrations and nitrate reduction in the eastern tropical North Pacific: Limnology Oceanography, v. 17, p. 885-900.
Cloud, P. C., 1976, Beginnings of biospheric evolution and their biogeochemical consequences Paleabiology, v. 2, p. 351-387.
DeVol, A. H., 1978, Bacterial oxygen kinetics as related to biological processes in oxygen deficient zones of the oceans: Deep-Sea Research, v. 25, p. 137-146.
Eppley, R. W., Rogers, J. N., and McCarthy, J. J., 1969, Half saturation constants for uptake of nitrate and ammonium by phytoplankton: Jour. Phycology, v. 5, p. 333340.
Fanning, K. A., and Pilson, M. E. Q., 1972, A model for the anoxic zone of the Cariaco Trench: Deep-Sea Research, v. 19, p. 847-863.
Fenchal, T., and Blackburn, T. H., 1979, Bacteria and Mineral Cycling: London, Aca~lemic Press, 225 p.
Goering, J. J., 1968, Denitrification in the oxygen minimum layer of the eastern tropical Pacific Ocean: Deep-Sea Research, v. 15, p. 151-164.
Garrels, R. L., and Perry, E. A., Jr., 1974, Cycling of carbon, sulfur, and oxygen through geologic time, in Goldberg, E., ed., The Seas, V. 5, Marine Chemistry: New York, Wiley-Intersci., p. 303-336.
Harvey, H. W., 1957, The Chemistry and Fertility of Sea Water: Cambridge, Cambridge University Press, 234 p.
Hashimoto, L. K., Kaplan, W. A., Wofsy, S. C., and McElroy, M. B., 1983, Transformations of fixed nitrogen and N.O in the Cariaco Trench: Deep-Sea Research, v. 30 p. 575-590.
Holland, H. D., 1984, The Chemical Evolution of the Atmosphere and Oceans: Princeton, N.J., Princeton Univ. Press, 582 p.
Holser, W. T., 1984, Gradual and abrupt shifts in ocean chemistry during Phanerozoic time, in Holland, H. D., and Trendall, A. F., eds., Patterns of Change in Earth Evolution: Berlin, Dahlem Konferenzen, Springer-Verlag, p. 123-143.
Rester, D. R., 1975, Gases other than Carbon Dioxide, in Riley, G. A., and Skirrow, G., eds., Chemical Oceanography: London, Academic Press, p. 497-536.
Kump, L. R., and Garrels, R. M., 1986, Modeling atmospheric Of: in the global sedimentary redox cycle: Am. Jour. Sci., v. 286, p. 337-3G0.
Kuo, H. H., and Pierogis, G., 1973, The use of oxygen as a test for an abyssal circulation model: Deep-Sea Research, v. 20, p. 871-885.
Montgomery, R. B., 1958, Water characteristics of the Atlantic and World Ocean: DeepSea Research, v. 5, p. 134-148.
Qasim, S. Z., 1982, Oceanography of the northern Arabian Sea: Deep-Sea Research, v. 29, p. 1041-1068.
Quinby-Hunt, M. S., and Turekian, K. K., 1983, Distribution of the Elements in SeaWater: EOS, v. 64, p. 130-131.
Redfield, A. C., Ketchum, B. H., and Richards, F. A., 1963, The influence of Organisms on the Composition of Sea-Water, in Hill, M. N., ea., The Seas, v. 2, The Composition of Sea-Water and Comparative and Descriptive Oceanography: New York, Wiley-Intersci., p. 26-87.
Rhodes, D. C., and Morse, J. W., 1971, Evolutionary and ecologic significance of oxygendeficient marine basins: Lethaia, v. 4, p. 413428.
Richards, F. A., 1957, Oxygen in the oceans, in Hedgepeth, J., ea., Treatise on Marine Ecology and Paleoecology: Geol. Soc. America Mem. 67, p. 185-238.
Richards, F. A., 1965, Anoxic basins and fjords, in Riley, J. P., and Skirrow, G., eds.: Chemical Oceanography: New York, Academic Press, v. 1, p. 611-G45.
Riley, G. A., 1951, Oxygen phosphate and nitrate in the Atlantic Ocean: gingham Oceanog. Colln. Bull., v. 13, p. 1-125.
Rutten, M. G., 1970, The history of atmospheric oxygen: Space Life Sci., v. 1, p. 1-13.
Ryan, W. B. F., and Cita, M. B., 1977, Ignorance concerning episodes of ocean-wide stagnation: Marine Geology, v. 23, p. 197-215.
Saino, T., Otobe, H., Wada, E., and Hattori, A., 1983, Subsurface ammonium maximum in the northern North Pacific and the Bering Sea in summer: Deep-Sea Research, v. 30, p. 1157-1171.
Schidlowski, M., and Junge, C. E., 1981, Coupling among the terrestrial sulfur, carbon and oxygen cycles: numerical modeling based on revised Phanerozoic carbon isotope record: Geochim. et Cosmochim. Acta, v. 45, p. 589-594.
Schidlowski, M., Junge, C. E., and Pietrek, H., 1977, Sulfur isotope variations in marine sulfate evaporites and the Phanerozoic oxygen budget: Jour. Geophys. Research, v. 82, p. 2557-2565.
Schulenberger, E., and Reid, J., 1981, The Pacific shallow oxygen minimum, deep chlorophyll maximum, and primary productivity reconsidered: Deep-Sea Research, v. 2S, p. 901-919.
Sillen, L. G., 1961, The physical chemistry of seawater, in Sears, M., ea., Oceanography: Am. Assoc. Adv. Sci., Washington, D.C., p. 549-581.
Stumm, W., and Morgan, J. J., 1970, Aquatic Chemistry: New York, Wiley, 583 p.
Taft, B. A., 1963, Distribution of salinity and dissolved oxygen on surfaces of uniform potential specific volume in the South Atlantic, South Pacific, and Indian Oceans: Jour. Marine Research, v. 21, p. ]29-146.
Thomas, W. H., 1966, On denitrification in the northeastern tropical Pacific Ocean: Deep-Sea Research, v. 13, p. 1109-1114.
Vaccaro, R. F., 1965, Inorganic Nitrogen in Sea Water, in Riley, J. P., and Skirrow, G. eds., Chemical Oceanography: New York, Academic Press, v. 1, p. 365-408.
Veizer, J., Holser, W. T., and Wilgus, C. K., 1980, Correlation of 13C/12C and "S/=S secular variations: Geochim. et Cosmochim. Acta, v. 44, p. 579-587.
Warren, B. A., 1981, The shallow oxygen minimum of the South Indian Ocean: DeepSea Research, v. 28a, p. 859-864.
Weiss, R. F., 1970, The solubility of nitrogen, oxygen, and argon in water and sea water: Deep-Sea Research, v. 17, p. 721-725.
Wilde, P., and Berry, W. B. N., 1982, Progressive ventilation of the Oceans--Potential for return of anoxic conditions in the Post-Paleozoic, in Schlanger, S. O., and Cita, M., eds., Nature and Origin of Cretaceous Organic Carbon-Rich Facies: London, Academic Press, p. 209-224.
1984, Destabilization of the oceanic density structure and its significance to marine "extinction" events: Palaeogeog., Palaeoclimatology, Palaeoecology, v. 48, p. 143-162.
1986, The role of oceanographic factors in the generation of global bioevents, in Walliser, O., ea., Global Bio-Events: Berlin, Springer-Verlag, p. 75-91.
Wooster, W. S., 1967, Further observations on the secondary nitrite maximum in the northeastern equatorial Pacific: Jour. Marine Research, v. 25, p. 154-161.
Wyrtki, K., 1961, The thermohaline circulation in relation to the general circulation in the oceans: Deep-Sea Research, v. 8, p. 39-64.
1962, The oxygen minimum in relation to ocean circulation: Deep-Sea Research, v. 9, p. 11-23.
| Climate: Non-Glacial | ||
|---|---|---|
| Ts | = Temperature mixed layer | = 25 (°C) |
| Td | =Temperature deep water | = 10 (°C) |
| dz | = Thickness of pycnocline | = 2900 (m) |
| dT/dz | = 0.0052 (°C/m) | |
| dT/dz | = 0.000052 (°C/cm) | |
| I /(Ts-Td) | = 0.067 (1 / °C) | |
| w/A | = 0.000003 (1/cm) | |
| w | (for A = 0.5 cm2/sec) | = 0.000001 (cm/sec) |
| Climate: Pre- or Post-Glacial | ||
| Ts | = Temperature mixed layer | = 25 (°C) |
| Td | = Temperature deep water | = 10 (°C) |
| dz | = Thickness of pycnocline | = 1400 (m) |
| dT/dz | = 0.0107 (°C/m) | |
| dT/dz | = 0.000107 (°C/cm) | |
| I /(Ts-Td) | = 0.067 (1 / °C) | |
| w/A | = 0.000007 (1/cm) | |
| w | (for A = 0.5 cm2/sec) | = 0.000003 (cm/sec) |
| Climate: Glacial | ||
| Ts | = Temperature mixed layer | = 25 (°C) |
| Td | = Temperature deep water | = 5 (°C) |
| dz | = Thickness of pycnocline | = 900 (m) |
| dT/dz | = 0.0222 (°C/m) | |
| dT/dz | = 0.000222 (°C/cm) | |
| I /(Ts-Td) | = 0.050 (1 / °C) | |
| w/A | = 0.000011 (1/cm) | |
| w | (for A = 0.5 cm2/sec) | = 0.000005 (cm/sec) |
Temperature and depths from Wilde and Berry (1982, 1984)
Technique and A value from Wyrtki (1961, p. 43-44)
Example calculation of redox profiles: after Wyrtki (1962)
| Depth | Temp | e-(w/A)Z | e-aZ | C3(e-aZ) | DO: mL/L |
| Meters | Celsius | calculated | |||
| I | II | III | IV | V | VI |
| O | 25 | 1.000 | 1.000 | 27.273 | 0.05 |
| 10 | 25 | 0.997 | 0.975 | 26.599 | 0.05 |
| 20 | 25 | 0.994 | 0.951 | 25.943 | 0.05 |
| 30 | 25 | 0.991 | 0.928 | 25.302 | 0.05 |
| 50 | 25 | 0.985 | 0.883 | 24.068 | 0.05 |
| 75 | 25 | 0.978 | 0.829 | 22.610 | - 1.10 |
| 100 | 25 | 0.970 | 0.779 | 21.241 | -2.17 |
| 125 | 24.4 | 0.963 | 0.732 | 19.954 | - 3.15 |
| 150 | 24.3 | 0.956 | 0.687 | 18.745 | - 4.06 |
| 200 | 24.0 | 0.942 | 0.607 | 16.543 | - 5.67 |
| 250 | 23.8 | 0.928 | 0.535 | 14.599 | - 7.03 |
| 300 | 23.5 | 0.914 | 0.472 | 12.884 | - 8.18 |
| 400 | 23.0 | 0.887 | 0.368 | 10.034 | - 9.90 |
| 500 | 22.5 | 0.861 | 0.287 | 7.815 | - 11.03 |
| 600 | 22.0 | 0.835 | 0.223 | 6.086 | - 11.70 |
| 700 | 21.5 | 0.811 | 0.174 | 4.740 | - 12.02 |
| 800 | 21.0 | 0.787 | 0.135 | 3.692 | - 12.07 |
| 1000 | 20.0 | 0.741 | 0.082 | 2.239 | - 11.62 |
| 1200 | 19.0 | 0.698 | 0.050 | 1.358 | - 10.71 |
| 1500 | 17.5 | 0.638 | 0.024 | 0.642 | - 8.93 |
| 2000 | 15.0 | 0.549 | 0.007 | 0.184 | - 5.70 |
| 2500 | 12.5 | 0.472 | 0.002 | 0.053 | - 2.65 |
| 3000 | 10.0 | 0.407 | 0.001 | 0.015 | 0.05 |
| 4000 | 10.0 | 0.301 | .000 | 0.001 | 0.05 |
| 5000 | 10.0 | 0.223 | .000 | .000 | 0.05 |
Input in mL/L equivalents Atmospheric Value
O--upper = 0.05 @ 50 m 2 mL/L or
O--lower = 0.05 @ 1000 m 1 % PAL
Constants-- Source
a = 0.000025 Wyrtki 1962
Ro = 7.50E-9 Wyrtki 1962
W = 0.000001 Table 1
A =0.5 Table 1
W/A =0.000003 Table 1
C3 =27.273 Appendix. A
C2 =- 41.578 Appendix. A
C1 =16.941 Appendix. A
Sample calculation of redox profiles using Wyrtki (1961, 1962) formulae
As noted in the text in eq (2) the concentration of oxygen can be modeled as:
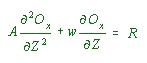 ......................................(2)
......................................(2)A = vertical exchange coefficient
w = vertical advection
R = RoeaZ
The solution of eq (2) for Os (oxidant) is:
Ox=C1 + C2e-(w/A)Z + C3e-aZ
where the constants of integration are:
C1 = Ox (@ upper boundary) - C2e-(w/A)Z (@upper boundary) - C3e-aZ(@ upper boundary);
C2 = [{Ox (@ upper boundary)--Ox (@ lower boundary)} -
{C3e-aZ (@ Upper boundary) +C3e-aZ (@ Lower boundary)} /
{e-(w/A)Z (@ Upper boundary) - e-(w/A)Z (@ Lower boundary)} ];
C3 = Ro/Aa(a - w/A)
Taken as constants are a = 0.000025 and Ro = 7.5 X 10~D.
Taken as constant for a particular climate (table 1) is the ratio (w/A), which is related to variation in temperature in the thermocline.
Table 2 gives a sample calculation of the redox profile with depth (column I) for conditions at 1 percent PAL and a non-glacial climate. Temperatures (column II) are assumed for the given climate as given in table 1. In this case, an equatorial location is assumed with a mixed layer from 0 to 100 m, a thermocline from 100 to 3000 m, and a deep isothermal layer below 3000 m. The change in temperature across the main thermocline is 15° Celsius with the temperature values assumed to decline in a linear manner. The oxygen concentration at the upper boundary is set at 0.05 mL/L derived from Henry's law for an atmosphere of 1 percent PAL. The depth of the upper boundary is chosen at 50 m as an average depth for the photic zone. The lower boundary is chosen at the base of the thermocline at 3000 m. Accordingly, the redox values vary from Henry's law saturation between 50 and 3000 m. Eq (2) is solved in steps (columns III, IV, V) to yield the redox values as oxygen equivalents as a function of depth (column VI). Plots of these values are used to construct redox profiles for particular conditions.